I love the movie Hidden Figures—it’s actually one of my favorites, and I could talk about it and about Katherine Johnson (the main character) for literally hours. Unfortunately, this article isn’t about cinema but about maths!
While browsing through YouTube, I found a video from Ellie Sleightholm that is absolutely mind-blowing.
Ellie is a YouTuber who posts videos diving into the maths behind different movies. Of course, I randomly stumbled upon one where she explains the maths behind Hidden Figures, and I just found myself totally absorbed.
First of all, she starts by solving the first equation we see in the movie:
(x² + 6x - 7)(2x² - 5x - 3) = 0
“Quite simple!” said I. “Let’s establish (x² + 6x - 7) = 0 & (2x² - 5x - 3) = 0 and solve with the quadratic formula.” But, of course, my ego needed to be crushed by someone.
Trigger Warning: The math I’m about to explain is super hard for an 8th-grade middle schooler. Though I didn’t think for a second about this method because my brain has assimilated so many automatisms at school.
What she did was only… only… factorize and solve a first-degree equation. (Told you, that was it.)
What I wanted to say here is that sometimes, our brain is so used to a specific method that we forget the basics. Although my method would have worked just fine, hers was 3x faster and more efficient.
Tip for later: When learning or solving a problem, think dumb first and THEN think smart.
Anyway, another thing she showed was the famous scene where Katherine stands up for her idea in front of her supervisor and says she prefers “Euclidean coordinates.”
Of course, Katherine… we ALL know what Euclidean coordinates are.
Well, it turns out it’s super simple:
- The Euclidean coordinate system is the “classic” way of representing our world mathematically in 3D. It comes with a classic x, y, z plane, where each point A has associated coordinates (xA, yA, zA).
-
The Frenet Frame, on the other hand, is the one Katherine uses. It describes the kinematic properties of a point moving along a differentiable curve in 3D Euclidean space. This means that instead of the beloved x, y, z, the point is described by:
- T (Tangent): the vector pointing in the direction of motion
- N (Normal): the vector directed 90° from the tangent
- B (Binormal): I had never seen this in my life, and I don’t want to explain something I barely understand, but all I know is that B = T × N

This representation of an object orbiting in space is actually super important because it allows you to describe motion at a certain time, not just position. With this model, you can predict where satellites will be three seconds after orbit, which is quite useful when you’re NASA. This method is also referred to as the TBN method.
Now, let’s end with the most important explanation.
In the movie, there’s this iconic scene where all the engineers and scientists are stuck in front of a mathematical equation on the board, and Katherine has a genius idea. She runs to her old department and grabs an old book describing an “old” method: Euler’s method.
While trying to understand it, I didn’t realize I was actually stepping into the dark, strange, fearful world of differential equations…
So, the basics: if you have a curve (shown below) that describes the trajectory of a spacecraft going to the Moon, you want to describe the curve mathematically so you can use it for different calculations and actually trace it. (This is only a simulation, so the curve is already drawn.)
The base of this method is the most GHETTO, RECKLESS, INSANE thing I have ever seen. The principle is super simple:
You have an equation where f is known, and y is an unknown variable:
dy/dt = f(x, t), y(t₀) = y₀
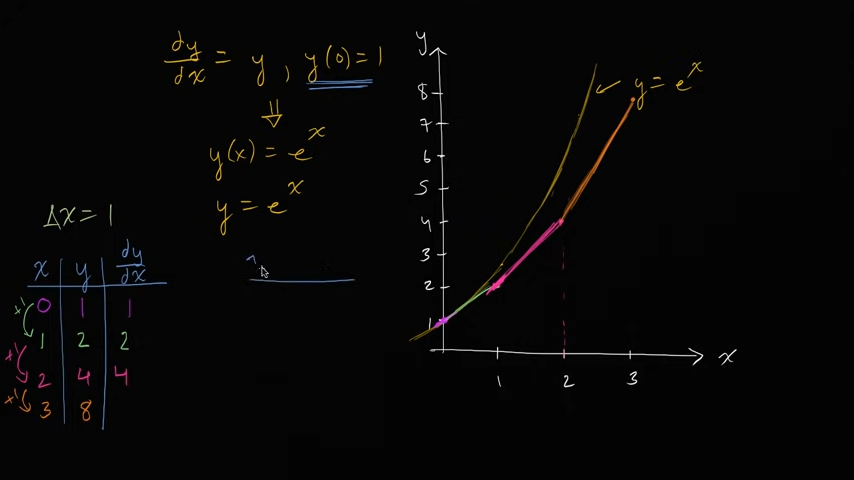
After watching another video from Khan Academy, I realized that this was miraculously related to what we are doing in math right now. (Photo above)
Basically, the method is:
- Calculate the tangent at a known point
- Add h to x
- Assume that y(x + h), which is the function of the tangent, is equal to the wanted curve, meaning that the newly created point is on or near the curve
- Repeat this until you eventually die
This is an awkward way of solving a problem because:
- It can be inaccurate
- OMG, it would take ages; like, I have no idea how NASA people did that at the time
However, it’s a numerical method (used more by computers) that helps determine the shape of a function or curve. Sometimes, it’s the only way to deal with a differential equation.
Anyway, I loved discovering all this cool stuff about maths and the way it’s portrayed in the film. Plus, I found a fascinating new YT channel and took my first step into the world of differential equations!
Here are the links to the videos. The images that have been used come from them.
https://www.youtube.com/watch?v=Et0lj0kbAk8 : Ellie’s YT channel
https://www.youtube.com/watch?v=q87L9R9v274 : the video from Khan Academy on Euler’s method, differential equations (AP Calculus)